
Previous versions of stb_truetype to 1.06 used a simple extension of the traditional scanline filling algorithm to compute horizontally-antialiased scanlines combined with vertical oversampling. The stb_truetype 1.06 algorithm (a re-invention of an algorithm generally credited to Levien's LibArt) computes the exact area of the concave polygon clipped to each pixel (within floating point precision) by computing the signed-area of trapezoids extending rightwards from each edge, and uses that signed-area as the AA coverage of the pixel. This provides more accuracy than sampling, although it is incorrect when shapes overlap (as it measures the area of the shapes within the pixel, not the fraction of the pixel that the shapes obscure), and is slightly faster than the old algorithm.
To determine if a point is within a concave-with-holes polygon, we classify each polygon edge with a direction (making each polygon a "winding"). Then, we cast a ray from the point to infinity, and count the edges it crosses, using a signed number for each edge (+1 in one direction, -1 in the other direction). If the final sum is non-zero, then the point is inside the polygon (assuming a non-zero fill rule).
The classic algorithm for filling such a polygon simply computes the same calculation incrementally.

For any scanline (e.g. the green lines above), we can start at negative infinity (i.e. anywhere to the left of the polygon) and scan along the line, counting crossings. Whenever the crossing count goes from zero to non-zero, we begin a filled region; whenever it goes from non-zero to zero, we end a filled region. For a closed polygon, it will always end up zero if it started at zero. (There are various things one must be careful about, e.g. if a vertex falls exactly on a scanline, we must be careful how we count those edges as 'crossing' that scanline. These are engineering details that don't affect the algorithm, and don't actually require much or any code if the right conventions are used.)
To actually implement this, a typical algorithm is:
I'm not sure if I read this algorithm somewhere or if I (re-)invented it myself, but it is a pretty straightforward extension. In the above algorithm, we treat scanlines as infinitely-thin 1D lines, but then we only sample the crossing-count at (say) pixel centers, despite the fact that we have more information along the horizontal axis.
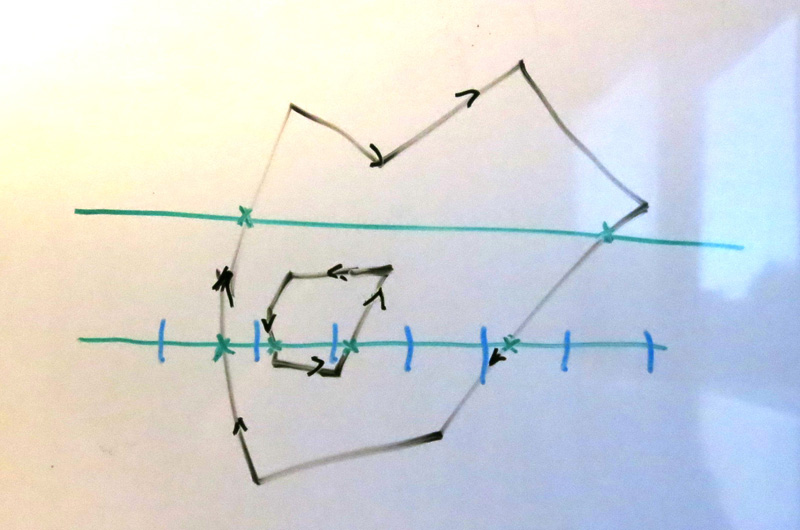
Here we've divided the lower "scanline" into multiple pixels, where each blue tick mark represents the boundary between pixels. We can easily measure how much of the scanline line segment between two pixels is "inside" the polygon, by coloring the parts of the line that are inside a different color:
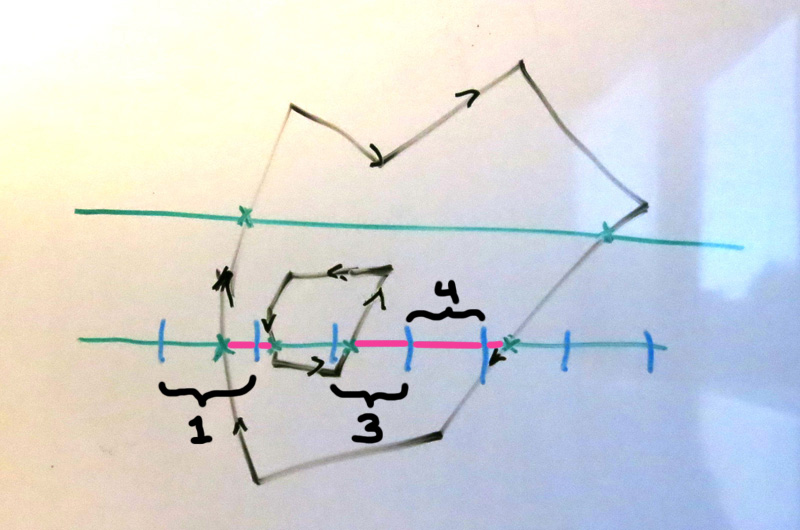
Here we can see that pixel #1 is about 25% pink, pixel 3 is about 80% pink, and pixel #4 is 100% pink. Thus we can determine that the (one-dimensional) anti-aliasing "coverage" of each of those pixels are 25%, 80%, and 100%.
The algorithm for computing this is identical to the previous algorithm; just the rule for how to fill pixels is different, as we have to track the fractional coverage of each "pixel" (line segment). Doing this is easy, though, since the edge crossings are always sorted left-to-right.
stb_truetype 1.05 and earlier use an algorithm like the above. Rather than computing the above on every scanline, the software "oversamples" along the y axis, placing 5 "scanlines" per row of pixels, and letting the computation for each one contribute only 1/5th of the "coverage" value computed for each pixel. (For small characters, stb_truetype oversamples by a factor of 15; 5 and 15 are used because they divide 255 evenly, so they avoid the need for any fixup of the final sum, which must be 0..255.)
The core idea behind the algorithm, using signed areas, came from Maxim Shemanarev's Anti-Grain Geometry source code; my coworker Fabian Giesen investigated that code to learn how the anti-aliased rasterizer worked, and came back with an incomplete understanding of the details, but a suspicion of that core idea. He shared the core idea with me, and I reworked a brand new algorithm from first principles based on it.
Edit: The idea itself appears to have reached AGG from FreeType which derived it from Ralph Levien's LibArt; whether it came from him originally or was a published algorithm is unknown.
Edit: I have now found other write-ups of this algorithm: here and here; however, I think this article is still generally clearer and more thorough, and some of the ideas are handled slightly differently.

as this merely requires computing a cross-product per edge.
Perehaps less frequently used, but based on the same principle, one can measure the area as the sum of the signed area of a number of right-trapezoids:
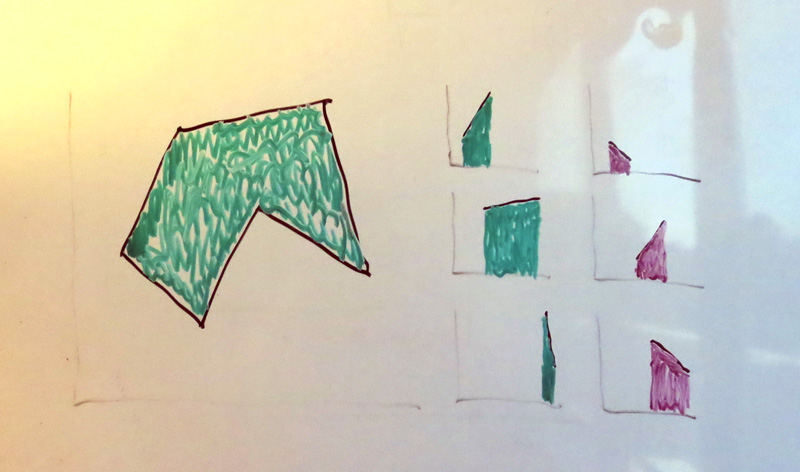
The area of an axially-aligned right-trapezoid is particularly easy to compute, and these fit very well into the scanline framework.
The differences here--beside the per-scanline processing discussed below--consist only of treating the scanline as 1-pixel tall (which slightly changes the rules for when edges are added and removed from the list), and omitting the need to sort the active edges from left to right.
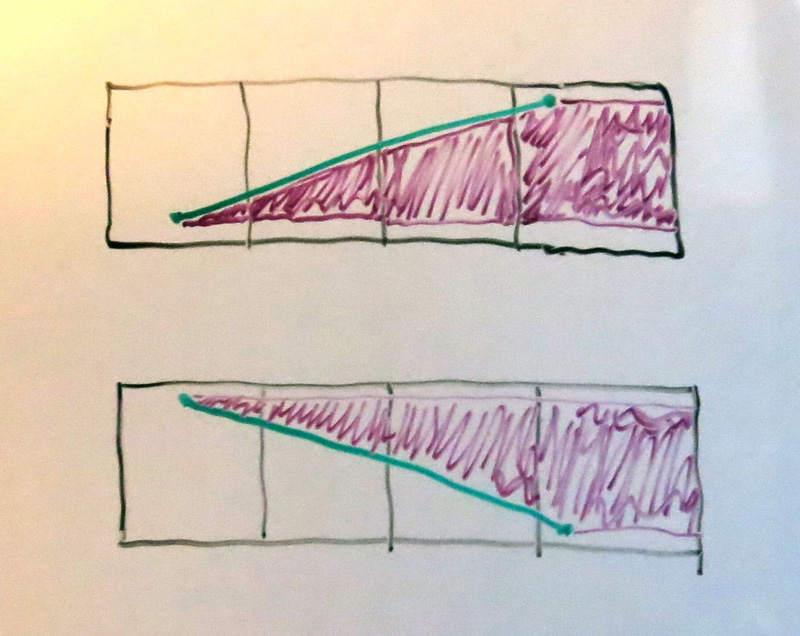
The basic premise is we want to use signed-trapezoid areas to compute the pixel areas. The illustration above showed trapezoids filled to the bottom edge, but we'll use trapezoids filled horizontally, to the right edge of the bitmap.
In other words, we want to compute something like the following (where color represents contribution from different edges, not the sign of the area):
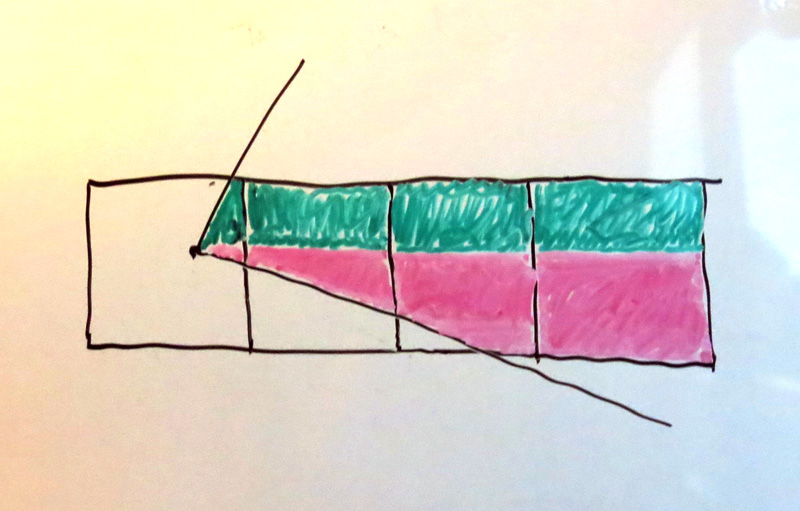
Here, each edge contributes to a right-extending trapezoid that covers multiple pixels, and theoretically extends infinitely far to the right. (The shapes within a single pixel may not be a trapezoid, e.g. the third pink shape, but it decomposes easily into a trapezoid and a rectangle.)
Later, we might close this polygon by drawing edges further to the right with the opposite signed area; these signed areas will extend rightwards, cancelling out the signed area in the pixels to the right of those new edges and producing 0-area per-pixel in those farther-right pixels.
Note first that we aren't trying to measure the area of the whole polygon, just the area coverage of each pixel, so we don't actually care about the signed area of the trapezoid from the edge all the way to the right; rather we just care about the signed area within each pixel.
Note second that the area in each pixel covered by the trapezoid for a given edge varies in the pixels that the edge passes through, but is constant for all of the pixels further to the right. (E.g. the three green rectangles are the same area, and if there were more pixels to the right, they would have the same coverage as the rightmost pixel.)
So the algorithm for the scanline is:
For each active edge:
For each pixel the edge intersects:
Compute the rightwards-trapezoid-ish area covering this pixel
Add the above area to the signed area for this pixel
For each pixel right of the edge:
Add the "height" of the edge within the scanline to the signed area for this pixel
The last line is because the areas to the right are always rectangles with width=1 pixel, so
the area is the height*1, i.e. just height.
Note that there is no need to traverse the active edges in any particular order, as the signed sums will be the same regardless, which is why the algorithm no longer keeps the active edges sorted horizontally.
To achieve efficiency, it is necessary to implement the last two lines efficiently; accumulating into all of the pixels to the horizontal edge of the bitmap would be inefficient with many shapes; with e edges crossing a scanline that is n pixels wide, we might have to perfom as many as e*n add operations.
To avoid this, we use the inverse of a cumulative sum table. If we make a table X and then later compute a cumulative sum S of X (where S[0] = X[0], S[n] = S[n-1] + X[n]), then we can create the effect of filling S[j..infinity] by simply writing a value into X[j]. Because everything is linear, we can likewise create the effect of adding a value height into S[j..infinity] by simply adding height into X[j].
In practice, we never compute the table S[]; the algorithm looks like this:
For one scanline: 1. Initialize arrays A, X to 0 2. Process e edges (see next section), summing areas into A & X 3. Let s = 0 4. For i = 0 to n do: 5. s = s + X[i] 6. a = A[i] + s 7. pixel[i] = 255 * a
This makes one linear pass over the whole pixel array, rather than the as many as e passes as the naive algorithm would.
The only thing missing from the algorithm above is how to compute the signed area coverage for any pixel which a given edge intersects. Computing this involves a large number of cases, which fortunately we can reduce to a small number of cases.
First, to avoid complexity, we test whether the edge's leftmost and rightmost x coordinates lie within the pixel range [0..n). In a font rasterizer, they normally always do; if they do not, we fall back to a less efficient algorithm that explicitly clip the edge's trapezoid to each pixel.
This means we never have to concern ourselves with the cases where the x coordinates lie outside the range of the A[] and X[] arrays, which reduces the cases to consider, i.e. removes the need for bounds-checking.
A given edge can have at most two intersections with a pixel, but those intersections can be with various combinations of the top and bottom and the sides. Additionally, an edge may have only one intersection (with any of the 4 sides), or no intersections at all.
To avoid this complexity, we can treat an intersection with the top the same as the top vertex lying within the pixel, and an intersection with the bottom the same as the bottom vertex lying within the pixel. The math is not identical as is, but we avoid a case explosion by handling them as the same kind of cases, by simply computing relative to the clipped endpoints, whether those be at the edges or somewhere inside.
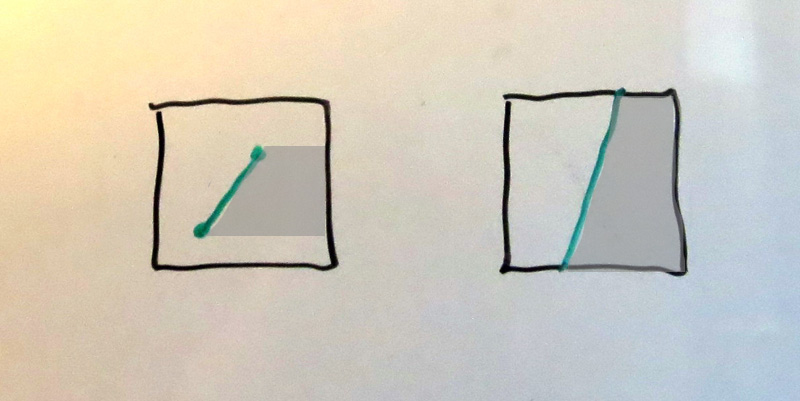
Here two of the four possible versions of this case are shown (the other two intersect only at the top or the bottom).
The calculation of the trapezoidal area covered to the right of these edges is straightforward. If the x coordinates are measured from the right side of the pixel, then the trapezoid's area is the height times the average of the two x-coordinates.
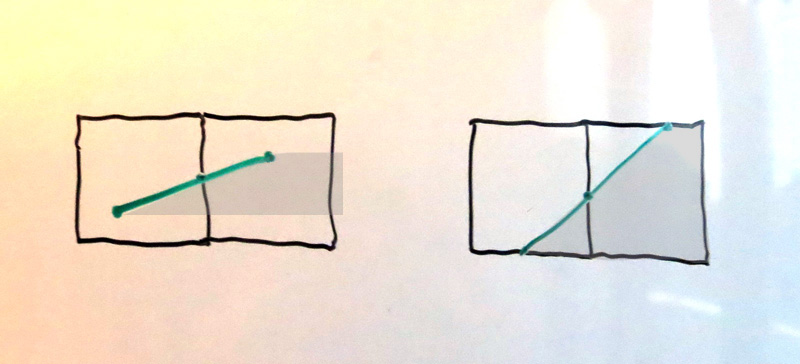
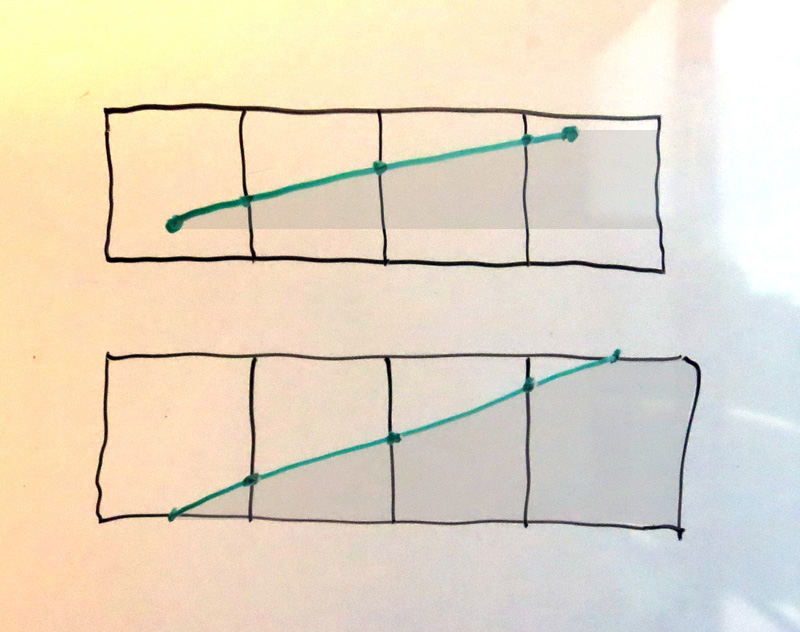
Computing the area covered by the right-extending trapezoids for these edges isn't much harder. In each case we must compute the intersections with the left and right sides of the pixels to evaluate the trapezoid formula mentioned above. However, once we compute the leftmost pixel's right-side intersection, the following intersections all increase linearly; in the same way that the vertical scanning algorithm simply steps the current x by dx/dy, so too can we simply step the y value of the side intersection by dy/dx.
But, even simpler than that, the area covered of each successive pixel itself increases linearly; that is, if there are 5 pixels covered, the area of pixels #1 and #5 are "arbitrary", but the difference between the area of pixel #2 and pixel #3 is the same as the difference between the area of pixel #3 and pixel #4; and that difference itself is also dy/dx.
Thus, handling this case requires:
1. Compute the intersection of the edge with right side of the leftmost pixel 2. Compute the area of the triangle in the leftmost pixel 3. Compute the area of the trapezoid in the second pixel 4. Process successive pixels, adding dy/dx to the area 5. Compute the intersection of the edge with left side of the rightmost pixel 6. Compute the area of the shape in the rightmost pixelalthough this is not exactly how the math is computed in stb_truetype.h.
Thus, we can write Case 2 strictly in terms of e.g. edges that slope NE-SW (regardless of direction); to handle edges that slope NW-SE, we simply flip the edge vertically (not swapping the endpoints, but actually flipping the y-coordinates and negating the slopes), and then use Case 2.
Alternatively, it may be possible to simply use the same code for both slopes, through judicious usage of absolute-value operations when computing the areas, and this may be faster as well, but I didn't try it.
{
int x,x1,x2;
float y_crossing, step, sign, area;
// covers 2+ pixels
if (x_top > x_bottom) {
// flip scanline vertically; signed area is the same
float t;
y0 = y_bottom - (y0 - y_top);
y1 = y_bottom - (y1 - y_top);
t = y0, y0 = y1, y1 = t;
t = x_bottom, x_bottom = x_top, x_top = t;
dx = -dx;
dy = -dy;
t = x0, x0 = xb, xb = t;
}
x1 = (int) x_top;
x2 = (int) x_bottom;
// compute intersection with y axis at x1+1
y_crossing = (x1+1 - x0) * dy + y_top;
sign = e->direction;
// area of the rectangle covered from y0..y_crossing
area = sign * (y_crossing-y0);
// area of the triangle (x_top,y0), (x+1,y0), (x+1,y_crossing)
scanline[x1] += area * (1-((x_top - x1)+(x1+1-x1))/2);
step = sign * dy;
for (x = x1+1; x < x2; ++x) {
scanline[x] += area + step/2;
area += step;
}
y_crossing += dy * (x2 - (x1+1));
scanline[x2] += area + sign * (1-((x2-x2)+(x_bottom-x2))/2) * (y1-y_crossing);
scanline_fill[x2] += sign * (y1-y0);
}
This algorithm runs slightly faster than the 5-times oversampled algorithm used in previous versions of stb_truetype.h. Since the 5-times-oversampled algorithm has to process 5 times as many scanlines, this may seem less speedup than expected; however, despite having the same overall framework, it has to do a lot more work.
The performance-relative differences are:
In particular, all of the code above for Case 2 is handled with oversampling by simply oversampling using the normal trivial code, whereas Case 2 involves a lot of processing per edge (although the per-pixel costs are fairly low for edges that cover many pixels).
The algorithm exactly computes the area of polygons intersecting a given pixel. However, if multiple overlapping polygons intersect the same pixel, it is measuring the area of the polygons, not the fraction of the pixel that is covered.

For example, if the entire shape above were within a single pixel, the algorithm would correctly compute the coverage of the pixel. However, if the interior hole were wound in the opposite direction, it would cease to be a hole, and the entire shape would be filled. In this case, the new algorithm would report the signed area of the shape as the sum of the outer shape and the inner shape, when the actual coverage of the pixel would simply be the area of the outer shape (the area covered by the inner shape is already counted in the outer shape's area, so that area is double-counted).
In practice large double-covered areas will be opaque, and the double-counting will be clamped to 100% coverage and have no effect. I believe in practice most errors due to double-counting will occur at concave corners where two shapes meet, leading to a single darker pixel in those areas. I believe that excessive darkening of concave corners will be unobjectionable.
It would be possible for someone to author a font where every character has the whole shape repeated twice or more; a traditional rasterizer, including the old stb_truetype one, would draw this identically to there only being a single copy of the shape, whereas the new one would draw all pixels with twice as much AA coverage (clamped), which would be an objectionable artifact. I do not expect to find fonts doing this in the wild, though. If it does turn out to be objectionable, the stb_truetype still has the old rasterizer available on a compile-time switch.